- SPITZE
- Grundlagen der CAE
- Teil 1 Was ist CAE-FEM-?
Serie: Grundlagen der CAE-Analyse für das Kunststoffproduktdesign
Teil 1 Was ist CAE-FEM-?
Wir vermitteln die Grundlagen der CAE und die wichtigsten Punkte der Finite-Elemente-Methode (FEM), die häufig in Analysen verwendet wird.
Inhalt
| 1. Was ist CAE? |
| 2. Voraussetzungen zur Nutzung der vollen Leistungsfähigkeit von CAE |
| 3. Was ist die Finite-Elemente-Methode (FEM)? |
| 4. Zusammenfassung |
Was ist CAE?
In den letzten Jahren ist die CAE-Analyse zu einem unverzichtbaren Werkzeug für die mechanische Konstruktion geworden. Kurz gesagt ist CAE (Computer-Aided Engineering) eine Technik, bei der Computer verwendet werden, um während des Produktentwicklungsprozesses bessere Designentscheidungen zu treffen. Dies geschieht, indem die Eignung von Designkandidaten bewertet und Hinweise zur Verbesserung gegeben werden.
Bevor Computer in der Fertigung eingesetzt wurden, konnten feine Details der Form und Struktur von Produkten nur durch den Bau echter Prototypen untersucht werden. Vor der Massenproduktion mussten viele Prototypen gebaut und auf Haltbarkeit und andere Eigenschaften getestet werden – ein Prozess, der sowohl teuer als auch zeitaufwändig war.
Vor diesem Hintergrund wurde CAE ursprünglich in den USA entwickelt. Die ersten kommerziellen Softwarepakete erschienen in den 1970er Jahren und das Feld entwickelte sich schnell, als die Leistungsfähigkeit von Computern in den 1980er Jahren und danach zunahm. Heute werden CAE-Techniken bereits in den frühesten Phasen des Design- und Entwicklungsprozesses eingesetzt – um mathematische und physikalische Modelle zu konstruieren, Produktspezifikationen, Leistung und Qualität mithilfe von Softwaretools vorherzusagen und Produktdesigns zu optimieren.
Obwohl CAE-Techniken ursprünglich zum Entwurf von Produkten auf Metallbasis wie Raketen und Flugzeugen verwendet wurden, sind diese Methoden heute auch für die Entwicklung von Kunststoffprodukten unverzichtbar. Diese Reihe beginnt mit einer allgemeinen Einführung in CAE und behandelt dann speziellere Themen: Unterschiede in den Eigenschaften verschiedener Kunststoffe, Simulationen von Herstellungsprozessen und Strukturanalysesimulationen für Kunststoffprodukte.
■ Wie werden CAE-Tools eingesetzt?
Heutzutage ist der gesamte Produktdesign- und Entwicklungsprozess digitalisiert, was mit den Begriffen CAD und CAM beschrieben wird. Dies ermöglicht eine nahtlose Integration von CAE.
CAD-Systeme (Computer-Aided Design) helfen bei der Verwaltung des Produktdesignprozesses. Die heute hauptsächlich verwendeten 3D-CAD-Tools ermöglichen die Gestaltung von Freiformflächen – eine deutliche Verbesserung gegenüber der vorherigen Generation von 2D-CAD-Tools, die nicht über genügend Freiheitsgrade verfügten, um eine solche Komplexität zu bewältigen. Durch die Verwendung von 3D-CAD-Daten in Fabrikproduktionslinien ist es sogar möglich geworden, Produktformen selbst mithilfe von CAD-Techniken zu entwerfen.
CAM-Systeme (Computer-Aided Manufacturing) bereiten die zur Herstellung von Produkten benötigten Informationen auf, beispielsweise Steuerdaten für NC-Werkzeugmaschinen. CNC-gesteuerte Werkzeugmaschinen sind computergesteuerte Instrumente zur automatischen Produktverarbeitung. Während bei konventioneller Bearbeitung menschliche Maschinisten manuell Drehknöpfe drehen und Hebel ziehen, um Schnitte zu machen und Löcher zu bohren, können NC-Werkzeuge mit numerischen Steuerdaten programmiert werden, um die Position und Abmessungen von Schnitten und jeden anderen Aspekt des Herstellungsprozesses zu automatisieren.
Kurz gesagt können mit CAD-Techniken erstellte Konstruktionsdaten in numerische Steuerungsdaten für CAM-Systeme umgewandelt werden, um den automatisierten Betrieb von Werkzeugmaschinen zu ermöglichen. CAD- und CAM-Tools werden häufig in Softwareprodukten zusammengefasst, die als CAD/CAM-Systeme bezeichnet werden. Die enorme Reduzierung herkömmlicher analoger Verarbeitungsschritte hat eine präzisere Konstruktion und effizientere Betriebsprozesse ermöglicht.
Ein typischer Entwurfs-/Entwicklungsablauf könnte darin bestehen, Produkte und Formen mit CAD-Tools zu entwerfen, die Entwurfsdaten mithilfe einer CAE-Analyse zu überarbeiten und Probleme bei der Produktherstellung zu beseitigen und die Daten anschließend zur Herstellung der Produkte an CAM-basierte NC-Werkzeugmaschinen zu senden.
Durch den Einsatz von CAE können Produktdesignkandidaten anhand von CAD-generierten Designdaten bewertet werden – bevor etwas hergestellt wird. Während das Produktdesign früher einen mühsamen Versuch-und-Irrtum-Zyklus erforderte – der die manuelle Anpassung hergestellter Prototypen beinhaltete und von der Erfahrung und Intuition erfahrener Handwerker abhängig war – kann heute der gesamte Prozess mithilfe von Computersimulationen analysiert werden. Die Versuch-und-Irrtum-Zyklen werden nicht nur beschleunigt, sondern die CAE-Analyse ermöglicht auch ein detaillierteres Verständnis der Ergebnisse, als dies normalerweise bei reinen Tests möglich ist.
■ Was ist mit CAE möglich?
Doch welche Arten von Analysen sind mit CAE möglich? Die heutigen CAE-Tools decken eine breite Palette von Anwendungsbereichen ab, die jeweils von einer Vielzahl maßgeschneiderter Softwarepakete abgedeckt werden. Genauer gesagt wird CAE in allen Bereichen der modernen Technologie eingesetzt – von mechanischen Produkten bis hin zu elektrischen und elektronischen Systemen, architektonischen Entwürfen, chemischen Prozessen, medizinischen Verfahren und vielem mehr – sowie in der Erforschung natürlicher Phänomene und bereichert viele Aspekte unseres täglichen Lebens.
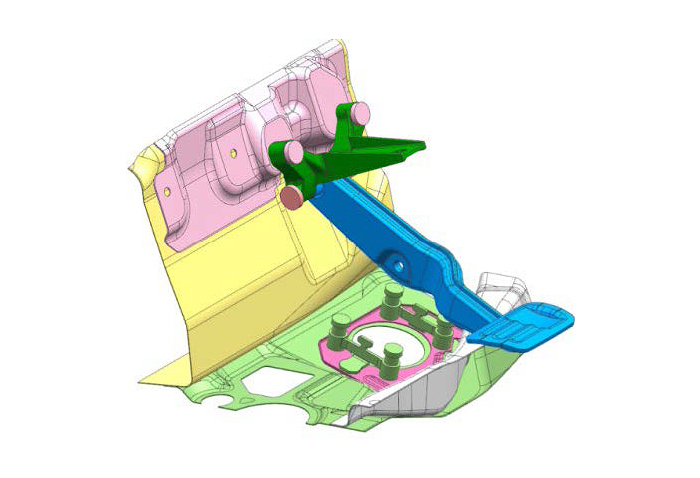
Beispielsweise wird im Maschinenbau und verwandten Bereichen mithilfe der CAE-basierten Strukturanalyse sichergestellt, dass bewegliche Produktteile nicht mit anderen Komponenten in Konflikt geraten – ohne dass Prototypen hergestellt werden müssen.
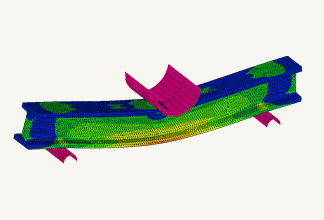
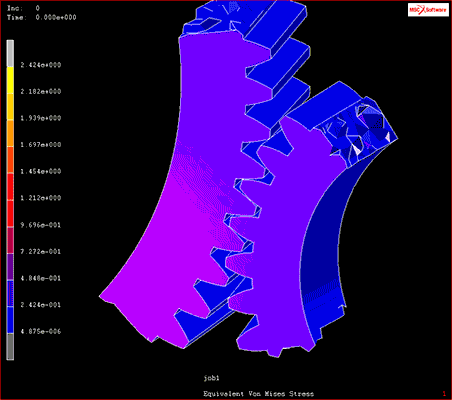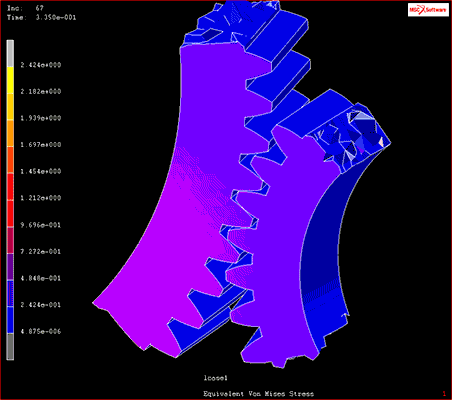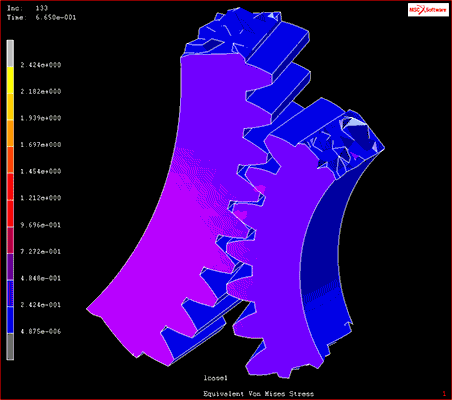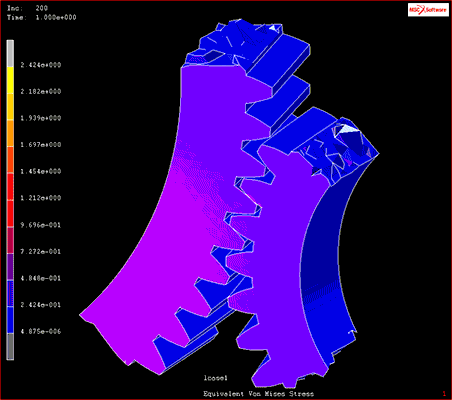 Abb. 1 Ergebnis der Mehrkörper-Dynamikanalyse
Abb. 1 Ergebnis der Mehrkörper-Dynamikanalyse
Quelle: Modell im Video „Kontaktanalyse“, „Störungs- und Schadensanalyse“ (abgerufen am 26. Februar 2021).https://www.mscsoftware.com/product/marc
*Modell im Video „Kontaktanalyse“, „Störungs- und Schadensanalyse“ (abgerufen am 26. Februar 2021).
https://www.mscsoftware.com/product/marc
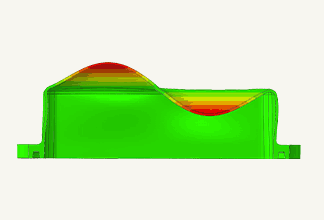
Sogar innerhalb des speziellen Teilbereichs der formbasierten Fertigung gibt es spezialisierte kommerzielle Softwarepakete für Kunststoffspritzguss, Metallguss, Druckguss, Presswerkzeuge und andere spezifische Bereiche. Die am häufigsten für Kunststoffspritzguss verwendete CAE-Technik ist die Flüssigkeitsanalyse, mit der Designer simulieren können, ob Kunststoffmaterialien ordnungsgemäß in Formen gespritzt werden können oder nicht.
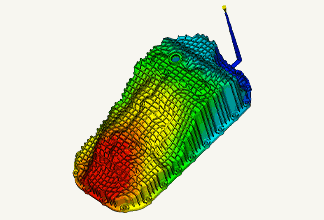
 Abbildung 2 Zustand der Harzfüllung durch Spritzgussanalyse
Abbildung 2 Zustand der Harzfüllung durch Spritzgussanalyse
■ Ein unverzichtbares Werkzeug für die moderne Fertigung
Die Verwendung von CAE-Tools zur Auswertung von CAD-generierten Designdaten reduziert die Anzahl der Prototyp-Iterationen, verkürzt die Entwicklungszeiten drastisch und senkt die Kosten. Da die Software immer leistungsfähiger und kostengünstiger wird und Computer immer leistungsfähiger werden, können CAD-ausgestattete Designer CAE-Tools verwenden, um Produkte selbst zu entwerfen und zu analysieren – ohne sich auf Fachingenieure für spezielle Analysen verlassen zu müssen. Die Einführung von 3D-CAD/CAM- und CAE-Systemen hat die Struktur der Fertigungsindustrie grundlegend verändert.
In der heutigen Welt, in der die Entwicklungszeiten immer kürzer werden und die Forderungen nach Kostensenkungen immer stärker werden, kann man mit Fug und Recht behaupten, dass die CAE-Analyse zu einem absolut unverzichtbaren Werkzeug für die moderne Fertigung geworden ist.
Voraussetzungen für die Nutzung der vollen Leistungsfähigkeit von CAE
So leistungsfähig und praktisch CAE-Techniken auch sein können, um die Kunst moderner CAE zu beherrschen, muss man sich mehr aneignen als nur ein paar Softwaretools. Man könnte hoffen, dass die Ergebnisse einer CAE-Analyse so einfach sind, dass sie für jeden sofort verständlich sind, unabhängig von seinem Hintergrund oder Fachwissen – aber das ist bei weitem nicht der Fall. Vielmehr erfordert die Fähigkeit, CAE-Ergebnisse genau zu interpretieren und in Konstruktionen zu integrieren, nicht nur Kenntnisse im Umgang mit Software, sondern auch Grundkenntnisse in der grundlegenden Ingenieurdisziplin der Materialmechanik und ein gründliches Verständnis grundlegender CAE-Techniken.
■ Grundlagen der Werkstoffmechanik
Die Materialmechanik ist eine Disziplin, die untersucht, wie sich Strukturkomponenten unter verschiedenen Arten angewandter Kräfte verformen und brechen. In der Materialmechanik werden Kräfte durch Vektoren dargestellt. Während Kräfte (wie die Schwerkraft) immer auf einen Körper wirken, sind sie bei einem ruhenden Strukturkörper ausgeglichen.
Die auf Strukturkomponenten wirkenden Kräfte umfassen sowohl äußere Kräfte (oder Lasten) als auch innere Kräfte, die innerhalb der Komponenten entstehen, um äußeren Kräften zu widerstehen. Zu den Arten äußerer Kräfte gehören Zuglasten, Drucklasten, Scherlasten, Biegelasten und Torsionslasten. Innere Kräfte werden mithilfe der Begriffe Spannung und Dehnung charakterisiert. Spannung wird als innere Kraft pro Oberflächeneinheit definiert. Da die auf Körper wirkenden inneren Kräfte unsichtbar sind, werden Berechnungen durchgeführt, indem Querschnittsscheiben durch Körper konzeptionell betrachtet werden und die Begriffe virtueller Querschnitt und Querschnittskoeffizient verwendet werden. Durch die Berücksichtigung der Kräfte pro Oberflächeneinheit kann der Einfluss der Materialeigenschaften vom Einfluss der Geometrie getrennt werden. Wenn die Materialeigenschaften bekannt sind, kann sich ein Konstrukteur beim Entwickeln eines Teils daher ausschließlich auf die Teilegeometrie konzentrieren.
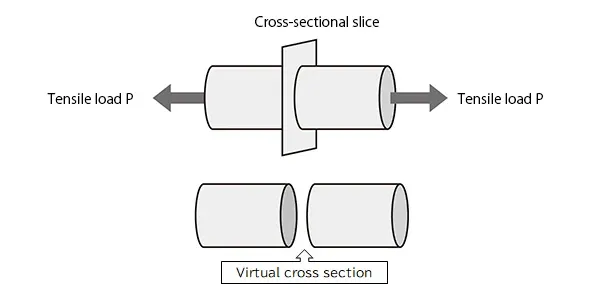 Abb. 3 Virtueller Querschnitt zur Spannungsberechnung
Abb. 3 Virtueller Querschnitt zur Spannungsberechnung
Betrachten wir als Beispiel einen Stab mit kreisförmigem Querschnitt, der von links und rechts gezogen wird, um eine Zugbelastung P von 100 N zu erzeugen. Unter der Annahme eines virtuellen Querschnitts mit einer Querschnittsfläche von 20 mm 2 ist die Spannung σ gegeben durch
σ=100/20 N/mm2=5 N/mm 2 =5MPa
σ=100/20 N/mm2=5 N/mm2=5MPa
d. h., die im Stab auftretende Spannung beträgt σ = 5 N/mm 2. Da sich herausstellt, dass die Dehnung die gleiche Einheit wie der Druck hat, wird sie häufig auch in MPa ausgedrückt.
Die Dehnung misst das Ausmaß, in dem sich Materialien verformen. Da die Dehnung numerisch mit einem Dehnungsmessstreifen gemessen werden kann (heutzutage auch durch Messen der Verformung der Probe in einem Video (DIC)), wird die Dehnung häufig zur Laborcharakterisierung realer Körper verwendet, während die Spannung häufig im Konstruktionsprozess verwendet wird.。
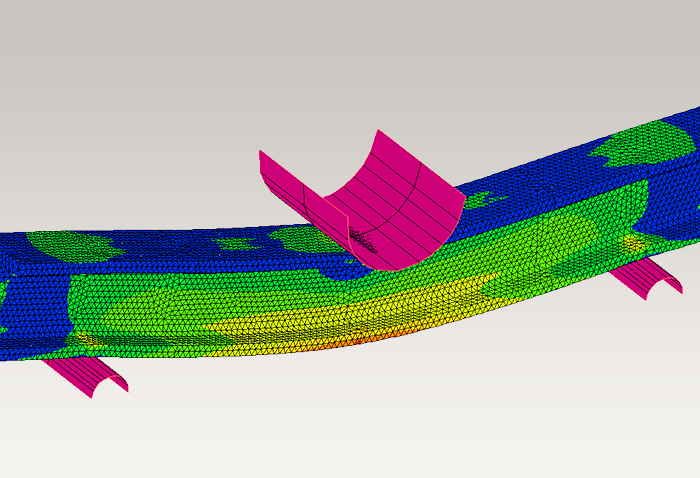
Obwohl Materialmechanikberechnungen für einfache Körper manuell durchgeführt werden können, weisen die meisten Körper in der realen Welt komplexe Strukturen auf, die sich mit manuellen Berechnungen nur äußerst schwer analysieren lassen. Beispielsweise ist die Spannung des Körpers, der in der Abbildung unten links dargestellt ist, manuell nicht schwer zu bestimmen. Das Hinzufügen auch nur eines einzigen Lochs zum Körper, wie rechts dargestellt, macht Materialmechanikberechnungen jedoch aufgrund der Spannungskonzentration in der Nähe des Lochs extrem kompliziert.
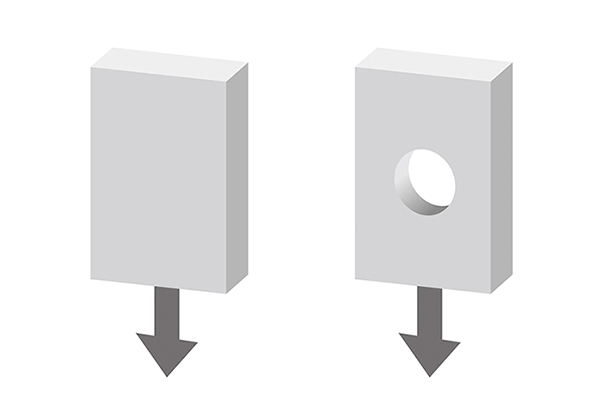 Abb. 4 Ein Beispiel, bei dem die Spannung leicht von Hand berechnet werden kann (links) und ein Beispiel, bei dem dies nicht möglich ist (rechts)
Abb. 4 Ein Beispiel, bei dem die Spannung leicht von Hand berechnet werden kann (links) und ein Beispiel, bei dem dies nicht möglich ist (rechts)
Für solche Fälle verwenden wir CAE-Tools. Mit CAE-Techniken können selbst Körper mit komplexen Formen problemlos analysiert werden.
■ Die drei wichtigsten Ansätze für CAE
Bei CAE-Analysen werden Körper und Strukturen mithilfe verschiedener Techniken in kleine Einheiten unterteilt, die leicht zu analysieren sind. So entstehen gekoppelte Gleichungssysteme, die numerisch gelöst werden können. Zur Simulation viskoser Flüssigkeiten und Feststoffe werden heute drei primäre CAE-Techniken verwendet: die Methode der finiten Differenzen, die Randelementmethode und die Methode der finiten Elemente.
(1) Die Finite-Differenzen-Methode (FDM) ist die älteste noch heute verwendete Analysemethode. Diese Technik, die häufig für die Fluidanalyse verwendet wird, diskretisiert die interessierenden Objekte auf einem orthogonalen Gitter, das als Finite-Differenzen-Gitter bezeichnet wird. Ein Nachteil der FDM-Techniken besteht darin, dass sie für die Analyse von Körpern mit gekrümmten Rändern oder anderen komplizierten Randbedingungen schlecht geeignet sind.
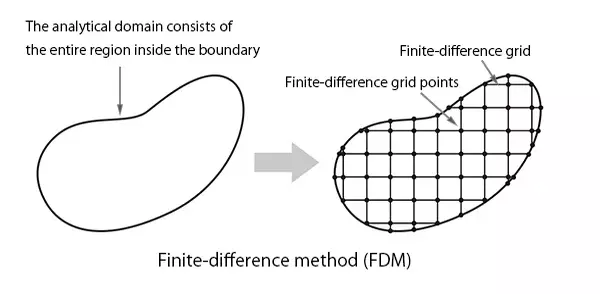 Abbildung 5 Finite-Differenzen-Methode (FDM)
Abbildung 5 Finite-Differenzen-Methode (FDM)
(2) Bei der Randelementmethode (BEM) werden lediglich die Grenzen von Materialbereichen für die rechnerische Analyse diskretisiert. Dieser Ansatz wird häufig zur Untersuchung der Konfiguration elektromagnetischer Felder verwendet.
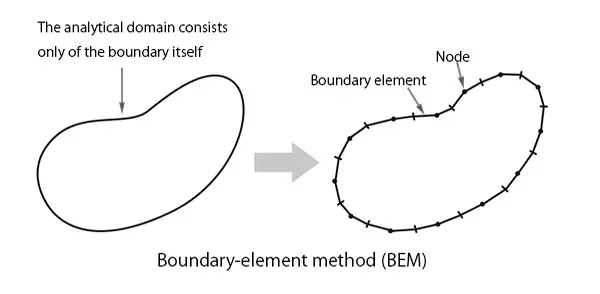 Abb. 6 Randelementmethode (BEM)
Abb. 6 Randelementmethode (BEM)
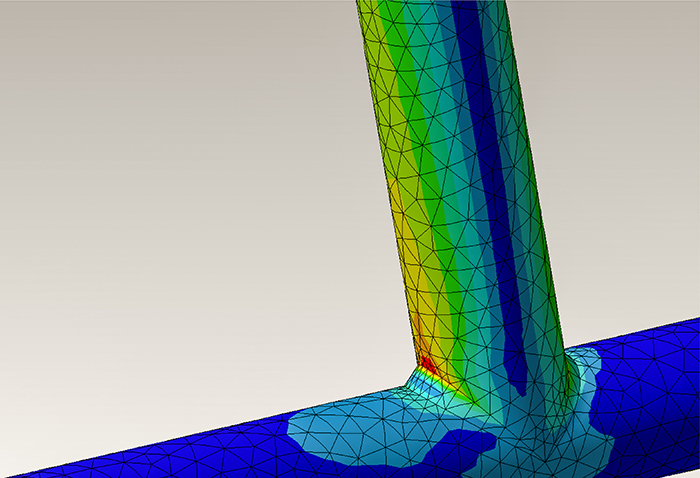
(3) Die Methode der finiten Elemente (FEM) ist heute der am häufigsten verwendete analytische Ansatz. Bei diesem Ansatz werden die zu untersuchenden Körper in Gruppen einfacher Formen wie Dreiecke oder Rechtecke unterteilt. Da mit diesem Ansatz nicht nur 2D-, sondern auch 3D-Systeme modelliert werden können, wird er häufig für Zwecke wie Strukturanalyse, thermische Analyse, Spannungsanalyse und Schwingungsanalyse verwendet.
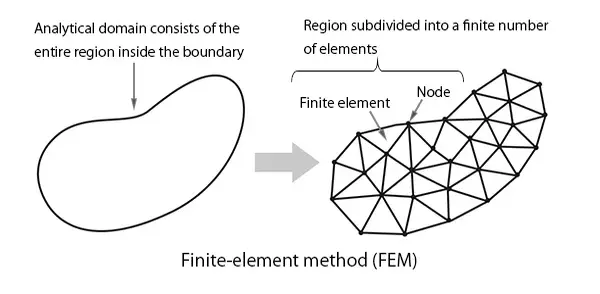 Abb. 7 Die Finite-Elemente-Methode (FEM)
Abb. 7 Die Finite-Elemente-Methode (FEM)
Was ist die Finite-Elemente-Methode (FEM)?
■ FEM-Techniken wurden erstmals bei der Strukturkonstruktion von Flugzeugen eingesetzt
Die Methode der finiten Elemente wurde ursprünglich in den 1950er Jahren entwickelt, um die Festigkeit von Tragflächenstrukturen bei der Konstruktion von Flugzeugen zu analysieren. Mit der Einführung von Düsentriebwerken wurden Flugzeugstrukturen immer komplexer, sodass die strukturelle Festigkeit mit ausreichender Genauigkeit berechnet werden musste.
Etwa zu dieser Zeit kamen auch universelle Digitalrechner auf den Markt, die eine schnelle Durchführung numerischer Berechnungen ermöglichten.
■ Die Grundphilosophie der Finite-Elemente-Methode
Bei der Methode der finiten Elemente werden Körper und Materialbereiche in Gruppen einfacher Formen wie Dreiecke und Rechtecke unterteilt. Eine solche Unterteilung wird als Netzdiskretisierung bezeichnet. Jede einzelne Komponente in einem Netz wird als Element bezeichnet, und jeder der Eckpunkte, aus denen die Elemente bestehen, wird als Knoten bezeichnet..
 Abb. 8 Ein Beispiel für die Netzaufteilung eines 2D-Modells
Abb. 8 Ein Beispiel für die Netzaufteilung eines 2D-Modells
Bei dreidimensionalen Analysen werden Körper in dreidimensionale (feste) Elemente zerlegt.
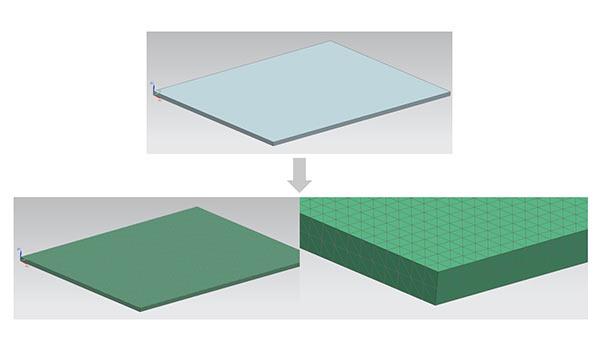 Abb. 9 Beispiel für die Netzaufteilung eines 3D-Modells
Abb. 9 Beispiel für die Netzaufteilung eines 3D-Modells
Wenn man die auf jedes Element einwirkenden externen Kräfte (wie Schwerkraft oder Druck) berücksichtigt, erhält man Gleichungen für das jeweilige Element. Da jedes Element mit mehreren Knoten verbunden ist, werden die auf jedes einzelne Element einwirkenden externen Kräfte über die Knoten auf seine Nachbarn und von dort auf die gesamte Struktur übertragen. Setzt man die Gleichungen für alle Elemente zusammen, erhält man ein simultanes System linearer Gleichungen, dessen Lösung die Verschiebung oder Spannung für jedes Element ergibt. Kurz gesagt löst die Methode der finiten Elemente schwierige Probleme, indem sie diese in einen Satz einfacher Gleichungen zerlegt und diese dann löst. Wenn die Methode zur Analyse komplizierter Probleme verwendet wird, kann die Zahl der gekoppelten Gleichungen natürlich ziemlich groß sein – in die Tausende oder gar Millionen –, sodass zur Lösung computergestützte Matrizenberechnungen erforderlich sind.
■ Wesentliche Merkmale der Finite-Elemente-Methode (FEM)
Die den Eckpunkten jedes Elements zugewiesenen Knoten werden als Elemente erster Ordnung bezeichnet. In manchen Fällen werden Knoten auch Zwischenpunkten innerhalb von Formen zugewiesen, wodurch Elemente zweiter Ordnung entstehen. Die Genauigkeit der Berechnungen kann durch Erhöhen der Anzahl der Knoten verbessert werden.
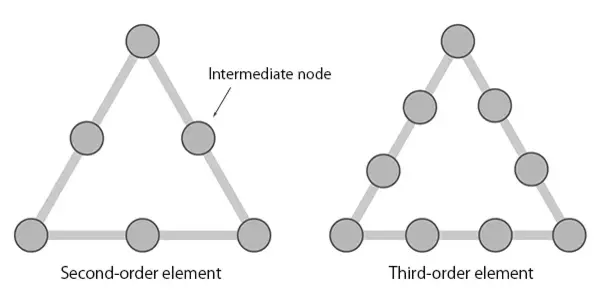 Abb.10 Unterscheidung finiter Elemente unterschiedlicher Ordnung
Abb.10 Unterscheidung finiter Elemente unterschiedlicher Ordnung
Alternativ kann die Genauigkeit auch durch Verfeinerung der Netzdiskretisierung verbessert werden, um die Anzahl der Elemente im Modell zu erhöhen. Jede dieser Verbesserungen führt dazu, dass sich die Näherungslösung mit finiten Elementen der exakten theoretischen Lösung des Problems annähert – auf Kosten einer längeren Rechenzeit. Andererseits wird es im Allgemeinen unmöglich sein, die tatsächlichen Formen komplexer Körper zu reproduzieren, egal wie genau wir unser Modell verfeinern. Letztendlich ist die CAE-Analyse nichts anderes als eine Technik zum Umwandeln komplizierter Probleme in rechnerisch handhabbare Modelle, um Näherungslösungen zu erhalten.
Es versteht sich von selbst, dass reale Designprozesse in einer begrenzten Zeit abgeschlossen werden müssen. Da Finite-Elemente-Analysen und andere CAE-Techniken eingesetzt werden, um die Entwicklungsvorlaufzeiten zu verkürzen, müssen die Genauigkeitsanforderungen, die an eine bestimmte Analyse gestellt werden, dem Zweck der Analyse und dem Kontext, in dem sie durchgeführt wird, angemessen sein.
Zusammenfassung
Die Einführung von 3D-CAD/CAM- und CAE-Analysen hat die Welt des Produktdesigns und der Fertigung verändert. Heute werden diese Techniken nicht nur für Flugzeuge und Autos, sondern auch für Kunststoffprodukte und eine Vielzahl anderer Zwecke eingesetzt; sie sind ohne Frage zu unverzichtbaren Werkzeugen für die moderne Fertigung geworden.
Gleichzeitig reicht es nicht aus, einfach nur Computer zu kaufen und Software zu installieren, um diese leistungsstarken Tools voll auszunutzen: Um das volle Potenzial der CAE-Techniken auszuschöpfen, ist ein gründliches Verständnis ihrer Grundprinzipien, der theoretischen Grundlagen und der praktischen Umsetzung erforderlich.
Nächster Teil: „Wichtige Punkte der Kunststoff-CAE – Unterschiede zu Metall-“.
◆Sie können die neuesten Versionsinformationen per E-Mail erhalten. Registrieren Sie sich hier.
Für weitere Informationen zu CAE kontaktieren Sie uns bitte.